Depois de explicar a Gravitação Universal, de Newton, Tatá volta alguns passos até as Leis de Kepler

ilustração: @paozinho_celestial
Parando para pensar na ordem cronológica dos fatos, eu comecei pelo fim e terminarei pelo início. E o início se dá nas Leis de Kepler. A partir delas, Newton formulou uma lei com a ajuda de Hooke, que gerou a maior confusão, mas isso vocês já sabem. De certa forma, a Lei da Gravitação Universal completa as formulações de Johannes Kepler, que enunciou as leis que descrevem os movimentos dos planetas ao redor do Sol.
Vamos começar com a primeira Lei de Kepler, Lei das Órbitas. Primeiro, é importante saber que os planetas não giram ao redor do sol de forma circular, mas sim elíptica, que, para facilitar, é apenas um círculo mais “esticado”. Isso significa que a distância entre o planeta e o sol varia ao longo da órbita, nunca é exatamente igual, e essa é a Lei das Órbitas, simples de ser entendida hoje, difícil de ser formulada nos tempos de Kepler.
Sabemos, graças a Galileu, que o Sol está no centro dessas órbitas, e que a Terra gira ao redor dele, não o contrário.
A segunda Lei é a das Áreas que diz que a linha (invisível) que conecta um planeta ao Sol varre áreas iguais em tempos iguais. Isso implica que, quando os planetas estão mais próximos do Sol, eles se movem mais rápido, e, quando estão mais distantes, se movem mais devagar. Isso gera um ciclo regular, que chamamos de ano, tendo a Terra como referencial.
A terceira, e não menos importante, é a Lei dos Períodos, que está diretamente ligada ao que falei acima: o tempo que o planeta leva para completar uma volta ao redor do Sol. Essa talvez seja um pouquinho mais difícil de ser expressa e entendida, mas o quadrado do período orbital (T2) é proporcional ao cubo do semieixo maior da sua órbita (a3). Tá bom, mas o que isso significa?
Cada planeta tem a sua própria órbita ao redor do sol, então temos 8 linhas imaginárias e no centro, há o Sol. Os planetas percorrem o caminho em cima da linha imaginária em torno do Sol, a órbita, e pela segunda lei de Kepler sabemos que às vezes os planetas estão mais próximos e às vezes mais longe do Sol. Quando estão mais longe, temos o semieixo maior da órbita.
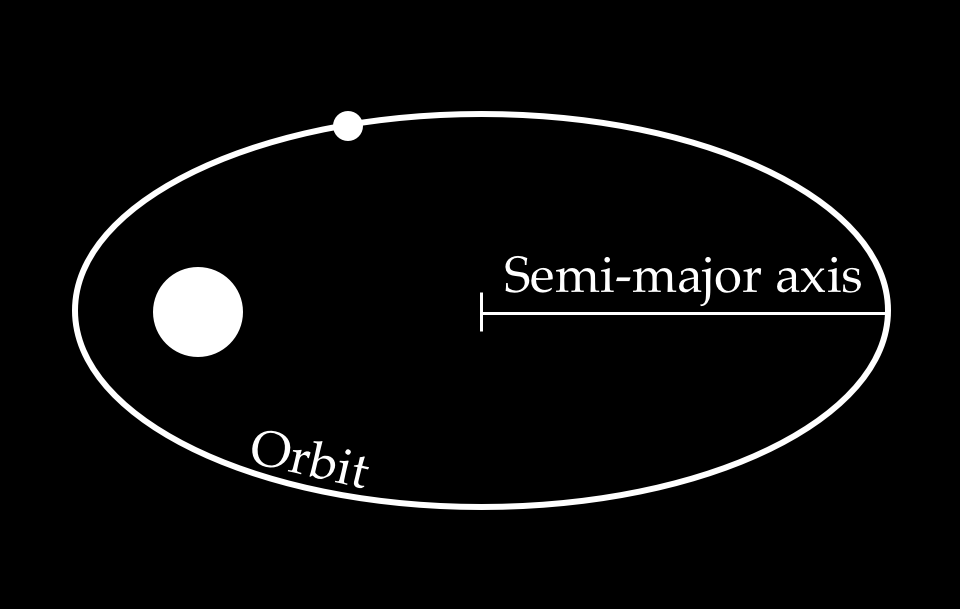
Representação da órbita de um planeta (Imagem: https://evgenii.com/blog/solar-system-with-proportional-distances/)
Vamos lá: pegue um papel e um lápis (estou esperando você fazer isso), tente desenhar uma órbita, um círculo mais achatadinho, depois trace uma linha na vertical, mas não no meio, mais para a direita. Viu que não ficou perfeito? Dividindo em dois, percebemos que um lado está maior e outro menor e esse lado maior é o semieixo que Kepler fala na sua terceira lei.
E a explicação da terceira lei é que quanto mais longe o planeta está do Sol, maior será o seu tempo orbital, ou seja, o tempo para completar uma volta ao redor do Sol.
Acho que não foi tão difícil assim, ou foi?
Mas ainda não acabamos!
Com a falta do conhecimento da gravidade, os antigos não conseguiam explicar direito. Kepler formula tudo isso, vai apresentar a alguém, e o povo pergunta: “como os planetas não escapam das suas órbitas quando estão ’andando‘ mais rápido?”. Me diz, você: como que explico isso?
Foi preciso vir Newton e expressar matematicamente a gravidade e a força gravitacional para sabermos que ela é inversamente proporcional ao quadrado da distância entre os objetos. Além de descobrir a constante gravitacional e a relação entre as massas. Só então ficou entendido que as leis de Kepler realmente estão certas e funcionam.